Skip to main content

ALS Implicit Collaborative Filtering

 Continuing on the collaborative filtering theme from my collaborative filtering with binary data example i’m going to look at another way to do collaborative filtering using matrix factorization with implicit data.

This story relies heavily on the work of Yifan Hu, Yehuda Koren, Chris Volinsky in their paper on Collaborative Filtering for Implicit Feedback as well as code and concepts from Ben Frederickson, Chris Johnson, Jesse Steinweg-Woods and Erik Bernhardsson.

Content:

  • Overview
  • Implicit vs explicit
  • The dataset
  • Alternating least squares
  • Similar items
  • Making recommendation

Overview

We’re going to write a simple implementation of an implicit (more on that below) recommendation algorithm. We want to be able to find similar items and make recommendations for our users. I will focus on both the theory, some math as well as a couple of different python implementations.

Since we’re taking a collaborative filtering approach we will only be concern ourselves with items, users and what items a user has interacted with.

Implicit vs explicit data

Explicit data is data where we have some sort of rating. Like the 1 to 5 ratings from the MovieLens or Netflix dataset. Here we know how much a user likes or dislikes an item which is great, but this data is hard to come by. Your users might not spend the time to rate items or your app might not work well with a rating approach in the first place.

Implicit data (the type of data we’re using here) is data we gather from the users behaviour, with no ratings or specific actions needed. It could be what items a user purchased, how many times they played a song or watched a movie, how long they’ve spent reading a specific article etc. The upside is that we have a lot more of this data, the downside is that it’s more noisy and not always apparent what it means.

For example, with star ratings we know that a 1 means the user did not like that item and a 5 that they really loved it. With song plays it might be that the user played a song and hated it, or loved it, or somewhere in-between. If they did not play a song it might be since they don’t like it or that they would love it if they just knew about.

So instead we focus on what we know the user has consumed and the confidence we have in whether or not they like any given item. We can for example measure how often they play a song and assume a higher confidence if they’ve listened to it 500 times vs. one time.

Implicit recommendations are becoming an increasingly important part of many recommendation systems as the amount of implicit data grows. For example the original Netflix challenge focused only on explicit data but they’re now relying more and more on implicit signals. The same thing goes for Hulu, Spotify, Etsy and many others.

The dataset

For this example we’ll be using the lastfm dataset containing the listening behaviour of 360,000 users. It contains the user id, an artist id, the name of the artists and the number of times a user played any given artist. The download also contains a file with user ages, geners and countries etc. but we’ll not be using that now.

Alternating Least Squares

Alternating Least Squares (ALS) is a the model we’ll use to fit our data and find similarities. But before we dive into how it works we should look at some of the basics of matrix factorization which is what we aim to use ALS to accomplish.

The idea is basically to take a large (or potentially huge) matrix and factor it into some smaller representation of the original matrix. You can think of it in the same way as we would take a large number and factor it into two much smaller primes. We end up with two or more lower dimensional matrices whose product equals the original one.

When we talk about collaborative filtering for recommender systems we want to solve the problem of our original matrix having millions of different dimensions, but our “tastes” not being nearly as complex. Even if i’ve viewed hundreds of items they might just express a couple of different tastes. Here we can actually use matrix factorization to mathematically reduce the dimensionality of our original “all users by all items” matrix into something much smaller that represents “all items by some taste dimensions” and “all users by some taste dimensions”. These dimensions are called latent or hidden features and we learn them from our data.

Doing this reduction and working with fewer dimensions makes it both much more computationally efficient and but also gives us better results since we can reason about items in this more compact “taste space”.

If we can express each user as a vector of their taste values, and at the same time express each item as a vector of what tastes they represent. You can see we can quite easily make a recommendation. This also gives us the ability to find connections between users who have no specific items in common but share common tastes.

If we can express each user as a vector of their taste values, and at the same time express each item as a vector of what tastes they represent. You can see we can quite easily make a recommendation.

Now it should be noted that we have no idea of what these features or tastes really are. We won’t be able to label them “rock” or “fast paced” or “featuring Jay-Z”. They don’t necessarily reflect any real metadata.

There are different ways to factor a matrix, like Singular Value Decomposition (SVD) or Probabilistic Latent Semantic Analysis (PLSA) if we’re dealing with explicit data.

With implicit data the difference lies in how we deal with all the missing data in our very sparse matrix. For explicit data we treat them as just unknown fields that we should assign some predicted rating to. But for implicit we can’t just assume the same since there is information in these unknown values as well. As stated before we don’t know if a missing value means the user disliked something, or if it means they love it but just don’t know about it. Basically we need some way to learn from the missing data. So we’ll need a different approach to get us there.

ALS is an iterative optimization process where we for every iteration try to arrive closer and closer to a factorized representation of our original data.

We have our original matrix R of size u x i with our users, items and some type of feedback data. We then want to find a way to turn that into one matrix with users and hidden features of size u x f and one with items and hidden features of size f x i. In U and V we have weights for how each user/item relates to each feature. What we do is we calculate U and V so that their product approximates R as closely as possible: R ≈ U x V.

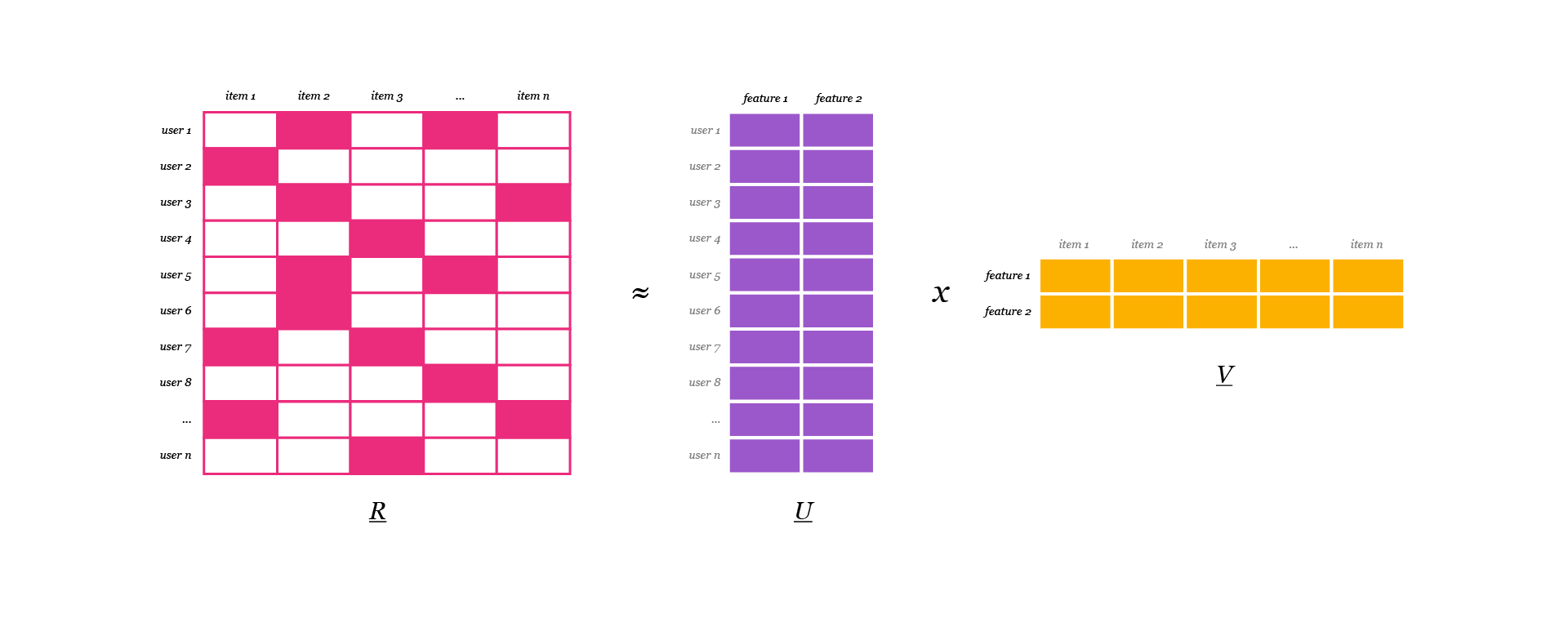
By randomly assigning the values in U and V and using least squares iteratively we can arrive at what weights yield the best approximation of R. The least squares approach in it’s basic forms means fitting some line to the data, measuring the sum of squared distances from all points to the line and trying to get an optimal fit by minimising this value.

With the alternating least squares approach we use the same idea but iteratively alternate between optimizing U and fixing V and vice versa. We do this for each iteration to arrive closer to R = U x V.

The approach we’re going to use with our implicit dataset is the one outlined in Collaborative Filtering for Implicit Feedback Datasets by Hu, Korenand and Volinsky (and used by Facebook and Spotify). Their solution is very straight forward so i’m just going to explain the general idea and implementation but you should definitely give it a read.

Their solution is to merge the preference (p) for an item with the confidence (c) we have for that preference. We start out with missing values as a negative preference with a low confidence value and existing values a positive preference but with a high confidence value. We can use something like play count, time spent on a page or some other form of interaction as the basis for calculating our confidence.

  • We set the preference (p):

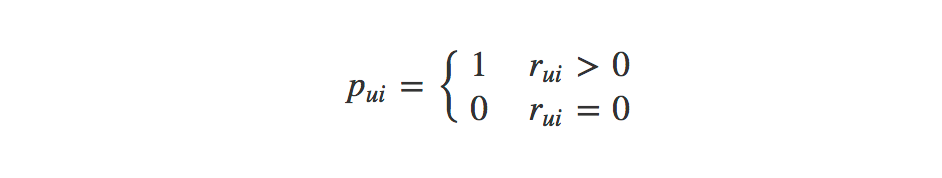
Basically our preference is a binary representation of our feedback data r. If the feedback is greater than zero we set it to 1. Make sense.

  • The confidence (c) is calculated as follows:

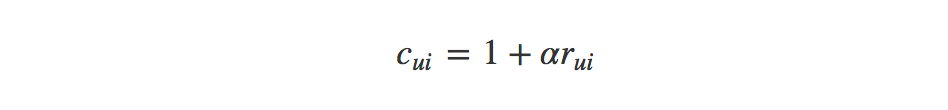
Here the confidence is calculated using the magnitude of r (the feedback data) giving us a larger confidence the more times a user has played, viewed or clicked an item. The rate of which our confidence increases is set through a linear scaling factor α. We also add 1 so we have a minimal confidence even if α x r equals zero.

This also means that even if we only have one interaction between a user and item the confidence will be higher than that of the unknown data given the α value. In the paper they found α = 40 to work well and somewhere between 15 and 40 worked for me.

The goal now is to find the vector for each user (xu) and item (yi) in feature dimensions which means we want to minimize the following loss function:

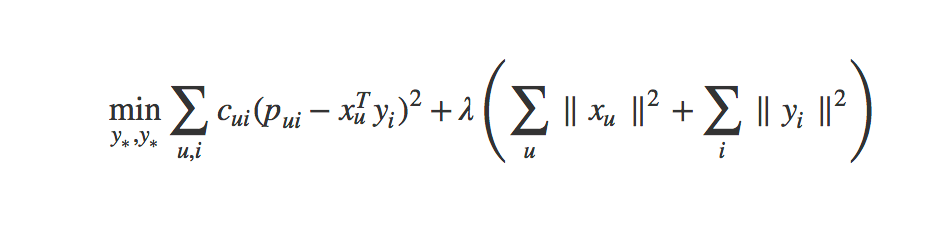
As the paper notes, if we fix the user factors or item factors we can calculate a global minimum. The derivative of the above equation gets us the following equation for minimizing the loss of our users:

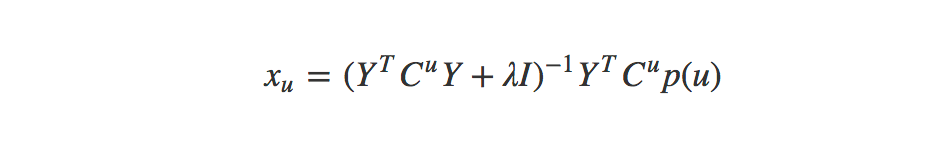
And the this for minimizing it for our items:

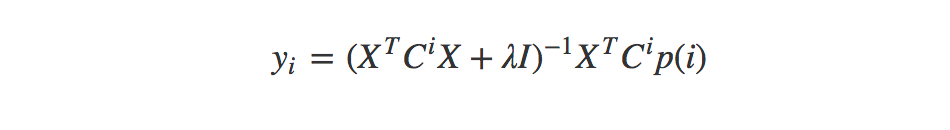
One more step is that by realizing that the product of Y-transpose, Cu and Y can be broken out as shown below:

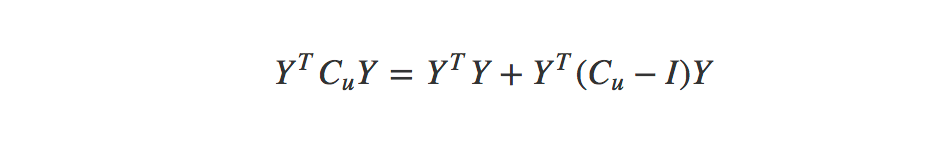
Now we have Y-transpose-Y and X-transpose-X independent of u and i which means we can precompute it and make the calculation much less intensive. So with that in mind our final user and item equations are:

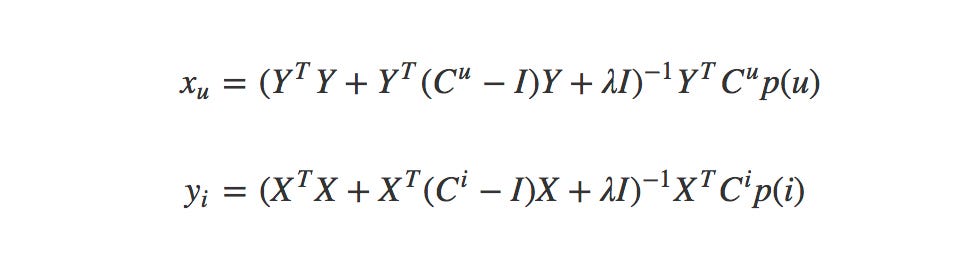
  • X and Y: Our randomly initialized user and item matricies. These will get alternatingly updated.
  • Cu and Ci: Our confidence values.
  • λ: Regularizer to reduce overfitting (we’re using 0.1).
  • p(u) and p(i): The binary preference for an item. One if we know the preference and zero if we don’t.
  • I (eye): The identity matrix. Square matrix with ones on the diagonal and zeros everywhere else.

By iterating between computing the two equations above we arrive at one matrix with user vectors and one with item vectors that we can then use to produce recommendations or find similarities.

Similar items

To calculate the similarity between items we compute the dot-product between our item vectors and it’s transpose. So if we want artists similar to say Joy Division we take the dot product between all item vectors and the transpose of the Joy Division item vector. This will give us the similarity score:

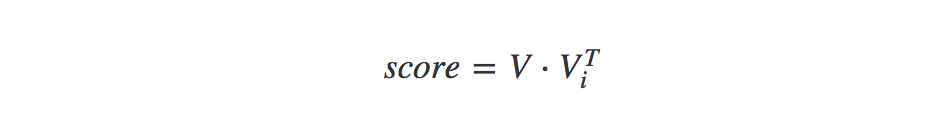
Making recommendations

To make recommendations for a given user we take a similar approach. Here we calculate the dot product between our user vector and the transpose of our item vectors. This gives us a recommendation score for our user and each item:

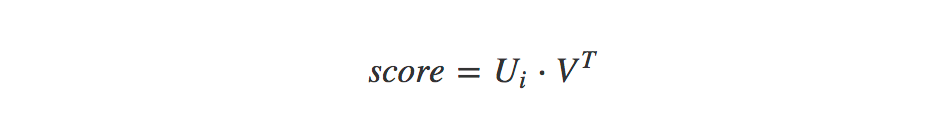
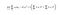
Comments

Post a Comment

Popular posts from this blog

Recommendation System and it's types

  Recommender systems are the systems that are designed to recommend things to the user based on many different factors. These systems predict the most likely product that the users are most likely to purchase and are of interest to. Companies like   Netflix , Amazon, etc. use recommender systems to help their users to identify the correct product or movies for them.    The recommender system deals with a large volume of information present by filtering the most important information based on the data provided by a user and other factors that take care of the user’s preference and interest. It finds out the match between user and item and imputes the similarities between users and items for recommendation.    Both the users and the services provided have benefited from these kinds of systems. The quality and decision-making process has also improved through these kinds of systems.   Check here a historical example of a recommendation engine  here....
Post a Comment
Read more

Co occurance Matrix

  This article attempts to provide a brief introduction to the co-occurrence matrix and its implementation in python. Given a document with a set of sentences in it, the co-occurrence matrix is a matrix form of representation of this document. To core idea of the co-occurrence matrix is to check if a particular word appears in the context of a focus word. Let us take an example to understand this better. Let us consider a document containing two sentences S1 and S2 as shown in Figure 1. There are three parts to creating a co-occurrence matrix. They are: Matrix of unique words Focus word Window length Matrix of unique words Let us create a matrix of all the unique words in the document as shown in Figure 2. All the values in the table are initialized to 0. Figure 2 Focus word & Window Length Once the matrix is created, we scan through each word (focus word) of each sentence of the document. We also determine the window length. This is the number of words we are considering, arou...
Post a Comment
Read more